三角形插值

2D平面中三角形

对于2D空间三角形，假设三个顶点分别为\(\mathbf{a} ,\mathbf{b},\mathbf{c}\)。则2D空间任意点都可以被下式表示出来：

\[ \mathbf{p}=\mathbf{a}+\beta(\mathbf{b}-\mathbf{a})+\gamma(\mathbf{c}-\mathbf{a})\tag{1} \]

可以理解为\(\mathbf{a}\)为起点，向量\((\mathbf{b}-\mathbf{a})\)和\((\mathbf{c}-\mathbf{a})\)构成的基张成一个平面空间。

整理可得：

\[ \mathbf{p}=(1-\beta-\gamma)\mathbf{a}+\beta \mathbf{b}+\gamma \mathbf{c} \tag{2} \]

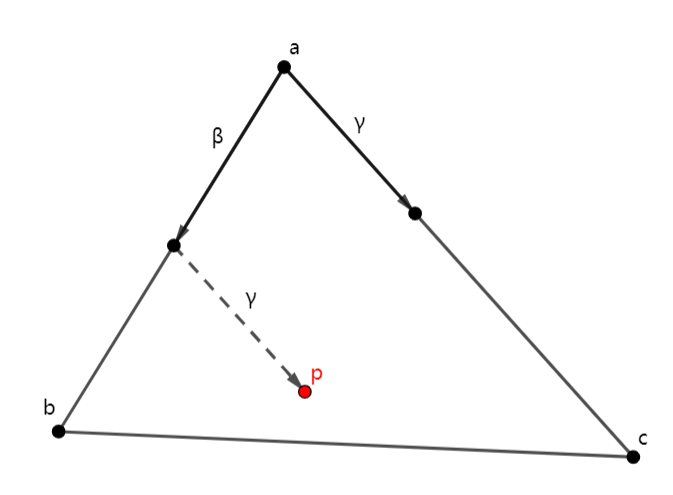
令\(\alpha\equiv 1-\beta-\gamma\)，得到重心坐标\((\alpha, \beta,\gamma)\)。当\(\mathbf{p}\)在三角形内部时，假设\(0<\beta<1\)，由相似三角形，有\(0<\gamma<1-\beta\)。因此，点\(\mathbf{p}\)在三角形内部当且仅当满足： \[ \begin{aligned} 0 &< \alpha < 1 \\ 0 &< \beta < 1 \\ 0 &< \gamma < 1 \end{aligned} \]

当\(p\)是重心时，重心坐标为\((\frac{1}{3},\frac{1}{3},\frac{1}{3})\)。

如何对于给定点\(\mathbf{p}=(x_p,y_p)\)，如何计算重心坐标？可以根据式\((1)\)解方程组。假设\(\mathbf{a}=(x_a,y_a)\)，\(\mathbf{b}\)、\(\mathbf{c}\)同理。 \[ \left[ \begin{matrix} x_b - x_a & x_c-x_a\\ y_b-y_a & y_c-y_a \end{matrix} \right]\left[ \begin{matrix} \beta\\ \gamma \end{matrix} \right]=\left[ \begin{matrix} x_p - x_a\\ y_p-y_a \end{matrix} \right]\tag{3} \]

除此之外，根据式\((1)\)的几何意义，可得重心坐标等价于面积比。

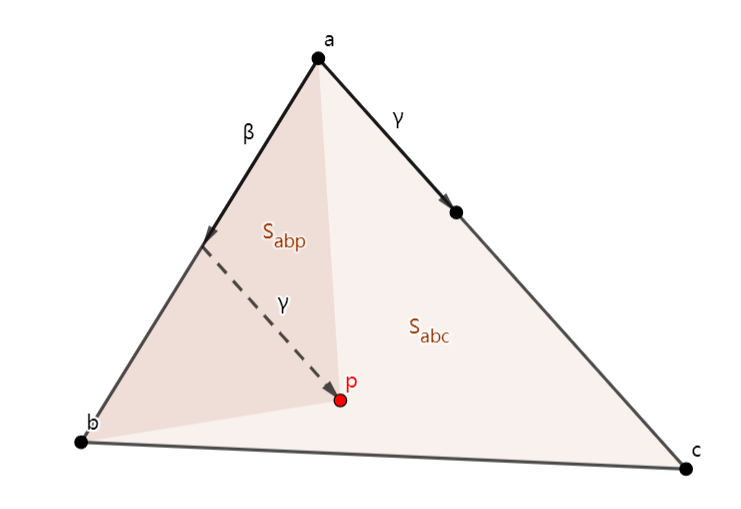
容易证明 \[ \frac{S_{abp}}{S_{abc}}=\frac{\gamma}{1} \] 可以使用叉乘求出三角形面积，或者使用一个叫边界函数的东西。对于边\(AB\)，其边界函数为： \[ E_{AB}(P)=(x_B-x_A)(y_P-y_A)-(x_P-x_A)(y_B-y_A) \] 这个函数值为三角形\(S_{ABP}\)的有符号面积的两倍，本质上就是一个行列式的结果。

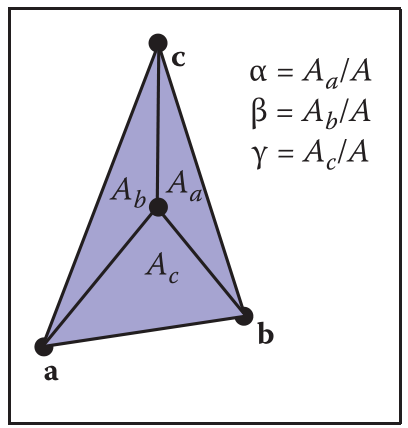
因此，各个重心坐标就可以表示为： \[ \begin{aligned} S = E_{ab}(c) \\ \alpha = \frac{S_{bcp}}{S_{abc}}=\frac{E_{bc}(p)}{S} \\ \beta = \frac{S_{cap}}{S_{abc}}=\frac{E_{ca}(p)}{S} \\ \gamma = \frac{S_{abp}}{S_{abc}}=\frac{E_{ab}(p)}{S} \end{aligned} \]

透视矫正

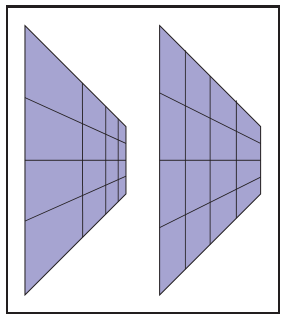
光栅化过程中，三角形中间的点的属性值将通过重心坐标插值出来。如果直接对屏幕空间的三角形插值将无法反映近大远小的效果。这种情况下，无论远近都被“均匀”地插值了，如下图所示，左边是正确的结果，符合近大远小的规律；右边是则是直接对屏幕空间插值，深度的效果消失了：

问题出在透视投影这一步。世界坐标系中两点\(\mathbf{q}\)、\(\mathbf{Q}\)构成的线段可以表示成如下（\(0\le k \le 1\)）：

\[ \mathbf{q}+k(\mathbf{Q}-\mathbf{q}) \]

对于某点\(\mathbf{p}\)，假如它的\(k=\alpha\)，可以表示为\(\mathbf{p}=\mathbf{q}+\alpha(\mathbf{Q}-\mathbf{q})\)，此时如果有某个属性\(I\)需要插值，那么该点的属性自然可以表示成：\(I_\mathbf{p}=I_\mathbf{q}+\alpha(I_\mathbf{Q}-I_\mathbf{q})\)。

Let's say \(\mathbf{p}\) 经过透视变换后（相当于乘上一个矩阵\(\mathbf{M}\)）：

\[ \mathbf{p}'=\mathbf{Mp}=\mathbf{Mq}+\alpha(\mathbf{MQ}-\mathbf{Mq})\equiv \mathbf{r}+\alpha(\mathbf{R}-\mathbf{r})\tag{1} \]

此时由于透视投影后的坐标（称为齐次坐标，homogeneous point），还要进行一次透视除法才能变成真正3维空间中的坐标（这个过程称为homogenized）。

\[ \frac{\mathbf{p}'}{\omega_{\mathbf{p}'}}=\frac{\mathbf{r}+\alpha(\mathbf{R}-\mathbf{r})}{\omega_\mathbf{r}+\alpha(\omega_\mathbf{R}-\omega_\mathbf{r})} \]

整理一下上式，化为如下形式：

\[ \frac{\mathbf{p}'}{\omega_{\mathbf{p}'}}=\frac{\mathbf{r}}{\omega_\mathbf{r}}+f(\alpha)(\frac{\mathbf{R}}{\omega_\mathbf{R}}-\frac{\mathbf{r}}{\omega_\mathbf{\mathbf{r}}})\tag{2} \]

其中

\[ f(\alpha)=\frac{\omega_\mathbf{R}\alpha}{\omega_{\mathbf{r}}+\alpha(\omega_\mathbf{R}-\omega_\mathbf{r})}\tag{3} \]

式\((2)\)中，\(\frac{\mathbf{r}}{\omega_\mathbf{r}}\)和\(\frac{\mathbf{R}}{\omega_\mathbf{R}}\)分别是\(\mathbf{q}\)和\(\mathbf{Q}\)透视投影后点！这意味者透视投影后的线段依旧是线段，同理还可以推出：对于在视锥体内的线段，投影后的线段点次序不变，平面投影后还是一个平面等非常有用的性质。

而且，原本\(\mathbf{p}\)的参数坐标是\(\alpha\)，经过投影后参数变为\(f(\alpha)\)！这里找到了投影前后参数并不相同，不能直接用\(f(\alpha)\)代替\(\alpha\)，但是可以通过两者的关系式求出\(\alpha\)。

\((2)\)式中投影后的点，可以理解为屏幕空间中的点。因为除了透视投影对\(\omega\)项发生修改，其余变换都不对\(w\)项修改，因此其余变换都不会改变\(\alpha\)。

已知参数\(f(\alpha)\)（它就是在屏幕空间中计算得到插值系数），就可以根据\((2)\)式推出\(\alpha\)。这个\(\alpha\)就是世界坐标系中的插值系数，就是我们想要的。这个过程就是透视纠正。

事实上，在屏幕空间对\(\frac{1}{\omega}\)插值等价于在世界坐标系中对\(\omega\)插值。证明如下：

\[ \frac{1}{\omega_\mathbf{r}}+f(\alpha)(\frac{1}{\omega_\mathbf{R}}-\frac{1}{\omega_\mathbf{\mathbf{r}}})=\frac{1}{\omega_\mathbf{r}+\alpha(\omega_\mathbf{R}-\omega_\mathbf{r})}=\frac{1}{\omega_{\mathbf{p}}} \]

所以，对于\(\mathbf{R}\)、\(\mathbf{r}\)之间的某点\(\mathbf{p}\)，想得到它的任意某种属性\(I_{\mathbf{p}}\)，直接对除以\(\omega\)后的\(I_\mathbf{R}\)、\(I_\mathbf{r}\)插值得到\(I_{\mathbf{p}}'\)：

\[ I_{\mathbf{p}}'=\frac{I_{\mathbf{r}}}{\omega_\mathbf{r}}+f(\alpha)(\frac{I_\mathbf{R}}{\omega_\mathbf{R}}-\frac{I_\mathbf{r}}{\omega_\mathbf{\mathbf{r}}})=\frac{I_\mathbf{r}+\alpha(I_\mathbf{R}-I_\mathbf{r})}{\omega_\mathbf{r}+\alpha(\omega_\mathbf{R}-\omega_\mathbf{r})}=\frac{I_\mathbf{p}}{\omega_\mathbf{r}+\alpha(\omega_\mathbf{R}-\omega_\mathbf{r})} \]

然后再对\(\frac{1}{\omega}\)直接在屏幕空间中插值，得到：

\[ 1'=\frac{1}{\omega_\mathbf{r}}+f(\alpha)(\frac{1}{\omega_\mathbf{R}}-\frac{1}{\omega_\mathbf{\mathbf{r}}})=\frac{1}{\omega_\mathbf{r}+\alpha(\omega_\mathbf{R}-\omega_\mathbf{r})} \]

最后：

\[ \frac{I_p'}{1'}=I_\mathbf{r}+\alpha(I_\mathbf{R}-I_\mathbf{r})=I_{\mathbf{p}} \]

可以看到\(\frac{I'}{1'}\)就是正确的插值结果。

上面只是线性情况下的透视矫正，但是和重心坐标插值是完全等价的。重心坐标插值可以视作两个线性插值的组合，因此矫正过程和上面相同。

综上，对于纹理坐标\((u,v)\)，可以如下计算正确的插值：（假设\(\alpha\)，\(\beta\)，\(\gamma\)是屏幕空间下的计算得到的重心坐标）：

\[ \begin{aligned} u' &=\alpha(\frac{u_a}{\omega_a})+\beta(\frac{u_b}{\omega_b})+\gamma(\frac{u_c}{\omega_c} ) \\ v' &=\alpha(\frac{v_a}{\omega_a})+\beta(\frac{v_b}{\omega_b})+\gamma(\frac{v_c}{\omega_c}) \\ 1' &= \alpha(\frac{1}{\omega_a})+\beta(\frac{1}{\omega_b})+\gamma(\frac{1}{\omega_c}) \\ (u,v) &= (\frac{u'}{1'}, \frac{v'}{1'}) \end{aligned} \]

更进一步，可以证明，所有在三维空间里同x,y,z成线性关系的变量，不管是纹理坐标，顶点色或者法向还是其他，他们在屏幕空间里的插值规则都可以通过：插值前先/w，插值后要用时再 * w得到具体值，然后我们把这类三维空间里同x,y,z成线性关系的变量统进行统一的批量处理，和OpenGL的 attribute，varying处理方法相同。

作者：韦易笑 链接：https://www.zhihu.com/question/40624282/answer/87501965 来源：知乎

3D空间中三角形

3D空间重心坐标依旧满足式\((2)\)，只需使用叉乘求面积，然后计算面积比即可得到重心坐标： \[ \begin{aligned} \mathbf{n}_a=(\mathbf{c}-\mathbf{b}) \times (\mathbf{p} - \mathbf{b}) \\ \mathbf{n}_b=(\mathbf{a}-\mathbf{c}) \times (\mathbf{p} - \mathbf{c}) \\ \mathbf{n}_c=(\mathbf{b}-\mathbf{a}) \times (\mathbf{p} - \mathbf{a}) \\ \mathbf{n}=(\mathbf{b}-\mathbf{a}) \times (\mathbf{c} - \mathbf{a}) \\ \alpha=\frac{S_A}{S}=\frac{\mathbf{n}\cdot \mathbf{n}_a}{\parallel \mathbf{n}\parallel^2} \\ \beta=\frac{S_B}{S}=\frac{\mathbf{n}\cdot \mathbf{n}_b}{\parallel \mathbf{n}\parallel^2} \\ \gamma=\frac{S_C}{S}=\frac{\mathbf{n}\cdot \mathbf{n}_c}{\parallel \mathbf{n}\parallel^2} \end{aligned} \]

回顾一下：

\[ \mathbf{a}\times\mathbf{b}=(x_a,y_a,z_a)\times(x_b,y_b,z_b)=(y_az_b-y_bz_a,x_bz_a-x_az_b,x_ay_b-x_by_a) \]

Reference

• fundamentals of computer graphics 4th, 8.1.2: Triangle Rasterization
• 3D 图形光栅化的透视校正问题？