光栅管线中的变换

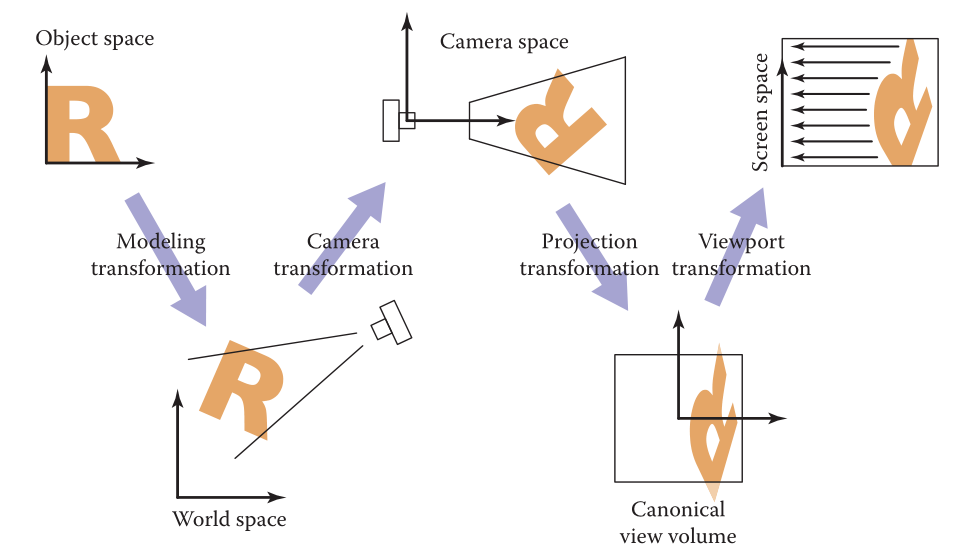
物体在呈现在屏幕前，要经过一系列的变换。前三步（Modeling transformation、Camera transformation、Projection transformation）都由我们自己完成，最后一步由显卡完成（包括裁剪、Viewport transformation、光栅化等步骤）。前三步也称为MVP变换。

下文均是建立在右手坐标系，相机朝向z轴负方向。

一、模型变换

模型变换就是将模型从模型坐标系变换到世界坐标系中。

位移矩阵： \[ T(x,y,z)=\left[ \begin{matrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \end{matrix} \right] \] 缩放矩阵： \[ S(x,y,z)=\left[ \begin{matrix} x & 0 & 0 & 0 \\ 0 & y & 0 & 0 \\ 0 & 0 & z & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \] 旋转矩阵：（略）

最后先缩放，再旋转，再位移，可得模型矩阵： \[ M=T R S \]

二、相机变换

相机变换是将世界坐标系下所有物体转换到以相机位置为原点的相机坐标系。由于相机朝向z轴负方向，转换后只有那些z坐标为负值的物体才会被处理。

只需给每个物体乘上相机模型变换矩阵的逆矩阵即可（相机一般不考虑缩放）： \[ V=M_{\text{camera}}^{-1}=R^{-1}T^{-1}=R^T(-T) \] 相机的旋转可以用欧拉角表示，可以用四元数表示，可以用lookat矩阵表示。只需转成旋转矩阵，转置即可。

三、透视变换

用于将相机坐标系中可见区域（即相机观察的范围）拉伸变换成为\([-1,1]^3\)的区域，便于后续处理。

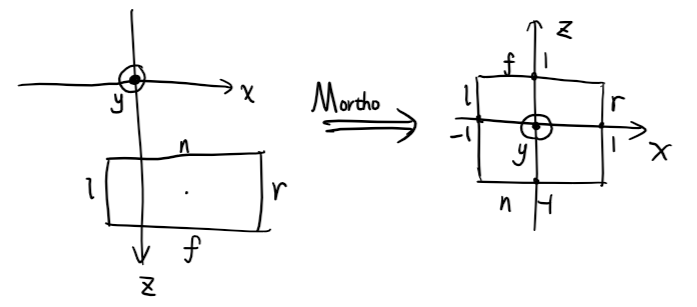
1、正交投影矩阵

相机朝向负半轴，z坐标越大代表离相机越近。为了符合直觉，这里会翻转一下z轴，使得z坐标越大代表离相机越远，这样旋性就从右手系到左手系了。

假设近平面（n）、远平面（f）、左平面（l）、右平面（r）、上平面（t）、下平面（b）坐标已知，有正交投影矩阵（注意缩放部分有个负项，用于翻转z轴）： \[ M_{\text{ortho}}= \underbrace{\left[ \begin{matrix} \frac{2}{|r-l|} & 0 & 0 & 0 \\ 0 & \frac{2}{|t-b|} & 0 & 0 \\ 0 & 0 & -\frac{2}{|n-f|} & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]}_{缩放} \underbrace{\left[ \begin{matrix} 1 & 0 & 0 & -\frac{l+r}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & \frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{matrix} \right]}_{位移} \]

2、透视投影矩阵

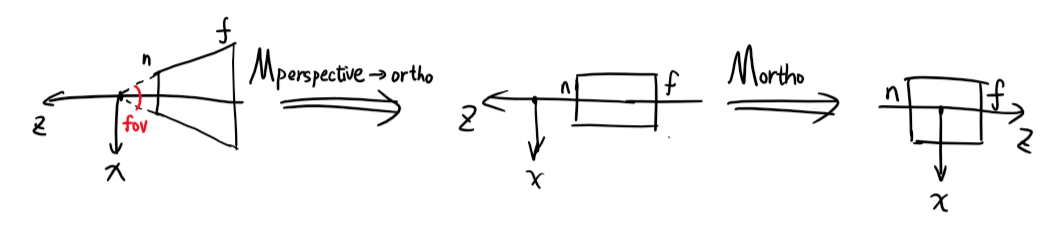
透视投影分两步，第一步透视变换将视锥体区域变换成矩形体区域，然后第二步应用正交矩阵即可。

透视变换参数有张角（fov，设为\(\theta\)）、宽高比（ratio，设为\(d\)）、远近平面距离（\(n\)，\(f\)，由于是距离，所以是绝对值）。

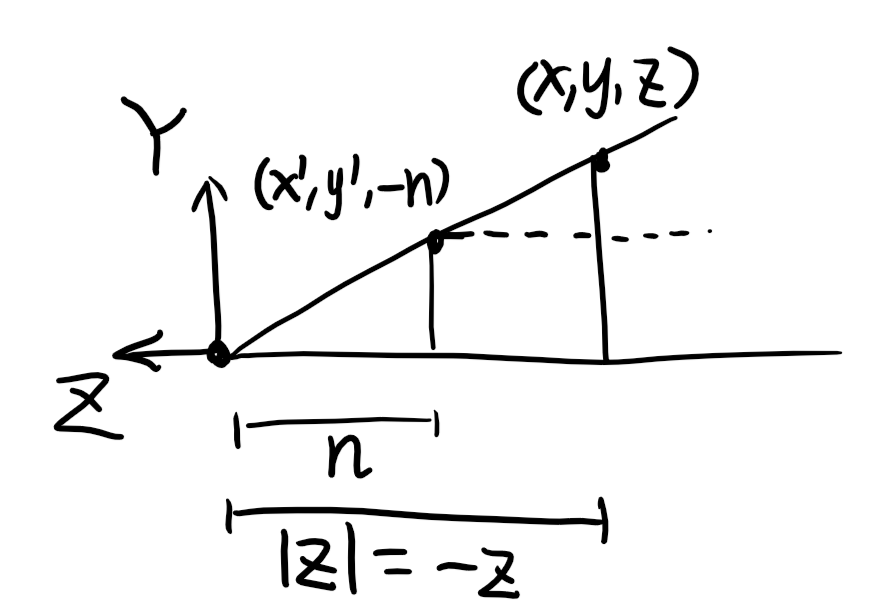
由于三维空间下该变换不是线性变换，无法用矩阵的乘法表；所以使用齐次坐标来表示，在四维空间下透视变换就是线性的了。以下是等价的表示： \[ \left[ \begin{matrix} x \\ y \\ z \\ w \end{matrix} \right]\equiv \left[ \begin{matrix} \frac{x}{w} \\ \frac{y}{w} \\ \frac{z}{w} \\ 1 \end{matrix} \right] \] 对于点\((x,y,z,1)\)，由相似三角形，经过变换以后有\(y'=\frac{n}{|z|}y\)、\(x'=\frac{n}{|z|}x\)。

$$ M_{ } =

\[ 由上式可以确定 \] M_{ }= $$ 其中\(A\)、\(B\)、\(C\)、\(D\)是未知数。

由变换前后，近平面和远平面点的z坐标不变这个性质，可得： \[ M_{\text{perspective} \to \text{ortho}} \left[ \begin{matrix} x \\ y \\ -n \\ 1 \end{matrix} \right]= \left[ \begin{matrix} nx \\ ny \\ Ax+By-nC+D \\ n \end{matrix} \right]= \left[ \begin{matrix} nx \\ ny \\ n\cdot (-n) \\ n \end{matrix} \right] \]

\[ M_{\text{perspective} \to \text{ortho}} \left[ \begin{matrix} x \\ y \\ -f \\ 1 \end{matrix} \right]= \left[ \begin{matrix} fx \\ fy \\ Ax+By-fC+D \\ f \end{matrix} \right]= \left[ \begin{matrix} fx \\ fy \\ f\cdot (-f) \\ f \end{matrix} \right] \]

解得\(A=B=0\)，\(C=n+f\)，\(D=nf\)

故 \[ M_{\text{perspective} \to \text{ortho}}= \left[ \begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & nf \\ 0 & 0 & -1 & 0 \end{matrix} \right] \] 而\(t=-b=\tan(\frac{\theta}{2})\cdot n\)，\(r=-l=t \cdot d\)。至此，所有量都知道了，可得 \[ M_{\text{perspective}}=M_{\text{ortho}}M_{\text{perspective} \to \text{ortho}} \]

3、透视投影带来的问题

经过透视投影后的坐标，称为齐次坐标，本质上是四维空间中的坐标。要执行一次透视除法，即各分量除以w分量，才是真正转换到NDC空间中。

透视除法将变换前后z的线性关系变成了非线性关系，将直线从0中间断开。下图是透视变换前后z的关系。

可以发现，如果有一个三角面片跨越了z轴零点，会导致值符号的突变。\(0<z<n\)时，\(z'\)小于0；\(z<0\)时，\(z'\)突然又大于0了。想象一下，一个三角形一个角明明穿过相机到相机的背面，但是计算出来的结果突然就变成在相机前面的无穷远处。当z坐标为0时，w分量也为0，此时一旦进行透视除法，会导致除0操作，搞出一个无穷出来，这将导致后面光栅化插值出非常鬼畜的结果。

如果所有点都处于视锥体范围内时，直接进行透视除法就不会有上面问题。因此乘完透视矩阵之后，不要急着进行透视除法，而是应该先将物体在视锥体外的部分裁剪掉，再进行透视除法。所有齐次坐标\(-w\le x,y,z\le w\)范围外的点都应当被裁剪掉。如果图省事，也可以只裁剪穿过近平面的点。

裁剪无需我们自己完成，显卡会帮我们完成。OpenGL会在顶点着色器到片元着色器之间进行裁剪，再进行透视除法。这就是为什么我们无需在顶点着色器中手动进行透视除法，因为OpenGL会在后面做一次透视除法。反而，如果我们在没裁剪前手动进行了透视除法，OpenGL就没办法在齐次坐标下进行裁剪，最后反而会出错。

下面将介绍如何进行裁剪。

3.1、裁剪三角形

传统剔除有三种，发生顺序依次是：视锥剔除、视口剔除、背面剔除。其中视锥剔除和视口剔除比较难以区分。视锥剔除发生CPU中，通过AABB盒、OBB盒等将物体包围起来，然后与视锥体做碰撞检测，直接剔除掉完全不可见的物体，粒度较大；视口剔除就是上面提到的裁剪：将视锥体外不可见部分剔除，可见部分留下。下面介绍的是视口剔除。

回顾一下，平面方程：\(N\cdot(q-p)=0\)，三维平面可以用四维向量表示为\(C=(N_x,N_y,N_z,-N\cdot q)\)，其中\(N\)是平面法线，\(q\)是平面上一点。如果齐次坐标\(p=(x,y,z,w)\)在平面上，当且仅当\(p\cdot C=0\)。如果\(w=1\)，\(N\)为单位向量，\(p\cdot C\)的几何意义就是三维点\(p\)到平面\(C\)的距离。\(p\cdot C\)的符号代表点在\(p\)的那一侧（大于0代表在法线指向一侧）。

裁剪三角形就是用一个平面分别截取三角形的两条边，本质上就是求线段和平面的交点。

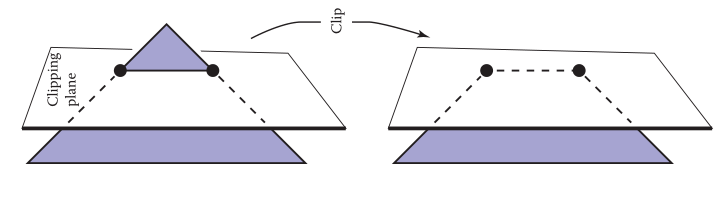
假设线段两端点的分别为\(a\)、\(b\)，线段上点\(p\)在平面\(C\)上，有 \[ \begin{aligned} p\cdot C=0 \\ (a+t(b-a))\cdot C = 0 \\ t = \frac{a\cdot C}{a\cdot C - b \cdot C} \end{aligned} \] 通过\(t\)可以求得边\(ab\)和平面的交点。而且，顶点除了位置信息，交点的属性也可以使用这个\(t\)插值出来。

有了上面基础后，下面介绍一个算法，叫做Sutherland–Hodgman多边形裁剪算法。

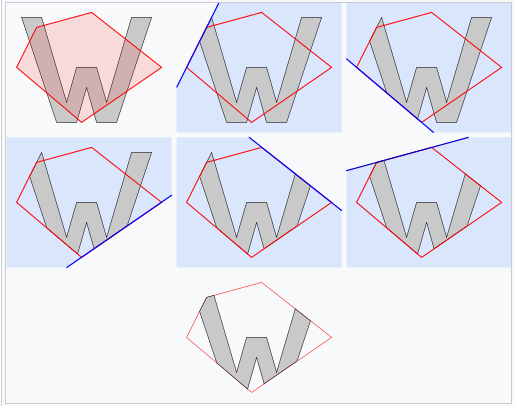
它主要思想就是依次使用裁剪平面对多边形裁剪，具体流程如下：

• 将多边形的所有顶点输入一个数组output作为原始输入；
• for循环，每次操作一条裁剪框边缘；
• 使用一个input数组接收output数组，output清零；
• 对于input，把第一个点置为当前点P，把最后一个点置为上一点S；
• 这时候S-P连线共有四种情况：
  • 线段两端均在平面可见侧（点乘大于0）：将P放入output
  • 线段两端均在平面不可见侧（点乘小于0）：不做操作
  • P在不可见侧，S在可见侧：将S-P与裁剪框交点L放入output
  • P在可见侧，S在不可见侧：先放入交点L再放入交点P
• 令S = P ，P取数组中下一点，重复操作直到遍历到数组中最后一点。

这样遍历所有裁剪面，就能获得新的顶点序列，对这个序列三角剖分即可。

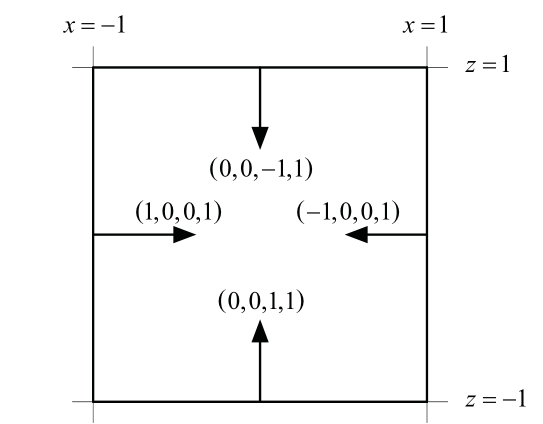
透视变换后，视锥体变成了统一的立方体，各个面的法线朝内指向零点，方程非常简单，分别是

平面	方程
near	\((0,0,1,1)\)
far	\((0,0,-1,1)\)
left	\((1,0,0,1)\)
right	\((-1,0,0,1)\)
top	\((0,1,0,1)\)
bottom	\((0,-1,0,1)\)

综上，用上面平面依次对三角形裁剪后，在组装起来，就可以实现视口剔除。

题外话，可以指定容易的平面进行裁剪，不一定只能是视锥体的各个面。如果想要实现一些特殊效果（如传送门、镜子），需要剔除虚拟相机前面遮挡的物体，就可以用上面的方法。当然，一个设定容易裁剪平面的更简单的方法请参考Referenece。

四、视点变换

视点变换就相当简单了，就是将NDC空间xy的\([-1,1] \times [-1,1]\)拉伸到屏幕大小\([0,w]\times [0,h]\)，z坐标不用管。这样处理后方便后续光栅化。

\[ M_{\text{viewport}}= \left[ \begin{matrix} \frac{w}{2} & 0 & 0 & \frac{w}{2} \\ 0 & \frac{h}{2} & 0 & \frac{h}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \]

Reference

• Oblique View Frustum Depth Projection and Clipping - Eric Lengyel
• 从零开始的软渲染器（2.5）- 再谈裁剪与剔除 - 知乎 (zhihu.com)