三维空间中的旋转
在介绍旋转之前,先分析一下两个概念:旋转和方向。方向即一个单位向量;旋转用来描述一个方向如何变换到另一个方向。在3维空间中,使一个方向变换到另一个方向的旋转有无数种,因为变换后的向量还可以绕以自己为旋转轴轴旋转。这意味着将旋转说成是一个方向变换到另一个方向的过程是不严谨的。准确地说,旋转描述的是坐标系到坐标系的变换。在3维空间中,只知道一个方向会变换到另一个方向,是无法唯一确定一个旋转的(当然也是可以构造出满足条件的旋转的,比如指定一个上向量)。
既然旋转是坐标轴的变换,旋转的本质就是旋转矩阵。旋转矩阵都是正交矩阵,但是正交矩阵不一定是旋转矩阵。
旋转矩阵对人来说不直观,因此有了一些方法,可以指定诸如角度、旋转轴等参数,表示相应的旋转。通过对参数的插值还能得到对旋转的插值,这是直接用旋转矩阵难以做到的。
下面介绍的方法(欧拉角、轴角、四元数)均可以表示所有的旋转,都可以生成任意旋转矩阵。这些方法的局限性(比如所谓的万向节死锁)并不是指无法表示某些旋转,而是在一些情景下会有不方便的情况。
下面描述的都是右手坐标系下的旋转,旋转方向是逆时针。
一、旋转矩阵
对于2维旋转:设旋转矩阵是\(M=\bigl[\begin{smallmatrix}a&b\\c&d\end{smallmatrix}\bigr]\)。假设逆时针旋转\(\theta\),分别对\((1,0)\)和\((0,1)\)作用旋转可得:
\[ \begin{aligned} \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] &= \left[ \begin{matrix} \cos\theta \\ \sin\theta \end{matrix} \right] \\ \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \left[ \begin{matrix} 0 \\ 1 \end{matrix} \right] &= \left[ \begin{matrix} -\sin\theta \\ \cos\theta \end{matrix} \right] \end{aligned} \]
解得
\[ M=\left[ \begin{matrix} \cos\theta & -sin\theta \\ \sin\theta & \cos\theta \end{matrix} \right] \] 对于3维旋转,可以类比上面的方法。使用待定系数法求出绕某个坐标轴的旋转矩阵,通过它们的组合就可以表示所有旋转: \[ M_x(\theta)=\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{matrix} \right] \]
\[ M_y(\theta)=\left[ \begin{matrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{matrix} \right] \]
\[ M_z(\theta)=\left[ \begin{matrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] \]
二、欧拉角
欧拉角就是按照次序分别绕3个轴旋转。例如XYZ规顺下(20°,30°,40°)代表的旋转就是先绕X轴旋转20°,再绕Y轴旋转30°,最后绕Z轴旋转40°。欧拉角又分静态欧拉角和动态欧拉角。静态欧拉角是每次都绕世界坐标系下的轴旋转,动态欧拉角则是每次都绕局部坐标系下的轴旋转(意味着每次旋转的旋转轴会受到前面旋转的影响,除了第一次,最开始局部坐标系和世界坐标系重合)。
下图是欧拉角的模型:
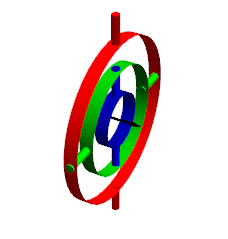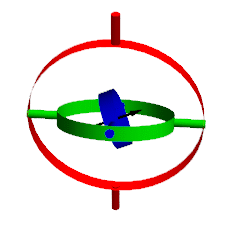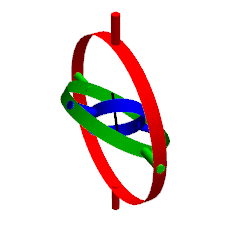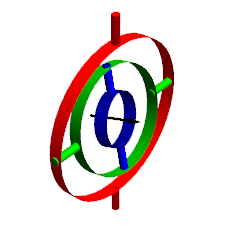
外圈(红色)控制绕Y轴旋转,中圈(绿色)绕X轴旋转,内圈(蓝色)绕Z轴旋转。外部圈的旋转会影响到内部圈,内部圈旋转不会影响到外部圈。从外到内旋转,每一圈都是绕局部坐标轴旋转的,这代表了YXZ规顺的动态欧拉角。类似的,从内到外旋转,内圈的旋转不会影响外圈,每次旋转都相当于绕的是世界坐标系下的轴。由此可以发现静态欧拉角和动态欧拉角的关系,它们其实就是旋转顺序不同而已。
综上,先绕世界坐标系Z轴旋转\(\alpha\)度,再绕世界坐标系X轴旋转\(\beta\)度,最后绕世界坐标系Y轴旋转\(\gamma\)度,等价于,先绕局部坐标系Y轴旋转\(\gamma\)度,再绕局部坐标系X轴旋转\(\beta\)度,最后绕局部坐标系Z轴旋转\(\alpha\)度。即ZXY规顺的静态欧拉角等价于YXZ规顺的动态欧拉角。其它规顺类似。
由于动态欧拉角作为参数更加直观,通过上面静态欧拉角和动态欧拉角关系,可以得到动态欧拉角的旋转矩阵: \[ R_{\mathbf{YXZ}}(\alpha,\beta,\gamma)=M_y(\alpha)\cdot M_x(\beta) \cdot M_z(\gamma) \] 欧拉角有个问题就是万向节死锁(Gimbal lock)。当任意两个旋转轴重合,就会少一个自由度。如下图,蓝圈绕的轴和红圈的重合,此时旋转红圈和旋转蓝圈效果是等价的。
这种情况下,同一个旋转可以被多个不同欧拉角表示。例如对于YXZ规顺动态欧拉角,(0°, 90°, 0°)和(-30°, 90°, 30°)是等价的旋转。这可能导致用欧拉角对旋转插值时出现诡异情况,例如从旋转(0°, 90°, 0°)插值到旋转(0°,0°,0°)和从旋转(-30°, 90°, 30°)插值到旋转(0°,0°,0°)不一样,即使旋转是等价,但是只有前者是预期的插值结果。

关于万向节死锁相关的内容可以看这个视频:欧拉角-万向节死锁问题直观理解,也可以看这个文章从代数角度的分析:bonus_gimbal_lock.pdf (krasjet.github.io)
三、轴-角旋转
旋转可以表示为绕一个特定的轴旋转\(\theta\)度,即参数为轴向量和旋转角度。3D空间中任意一个\(\mathbf{v}\)沿着单位向量\(\mathbf{u}\)旋转 \(\theta\) 角度之后的 \(\mathbf{v}′\) 为: \[ \mathbf{v}′=\cos(\theta)\mathbf{v}+(1-\cos(\theta))(\mathbf{u}\cdot \mathbf{v})\mathbf{u}+\sin(\theta)(\mathbf{u}\cdot \mathbf{v}) \] 证明思路是先将\(\mathbf{v}\)分别投影到平行于轴的分量\(\mathbf{v_{\parallel}}\)和垂直于轴的分量\(\mathbf{v_{\perp}}\)。然后对\(\mathbf{v}\)旋转等价于对两个分量进行同样的旋转再求和(旋转矩阵满足分配律)。这样\(\mathbf{v_{\perp}}\)就退化到平面的旋转,而\(\mathbf{v_{\parallel}}\)转了和没转一样。具体证明过程参考Reference里面的文章,写得超级好。
四、四元数
正如复数可以表示二维空间中的旋转,四元数可以表示三维空间中的旋转。每个单位四元数都对应一个旋转。
用四元数表示旋转和轴-角旋转有密切关系。为了不重复造轮子,下面只给出一些结论。具体原理和证明见Reference里面的文章,写得超级好。
和复数不同,四元数虽然满足结合律、分配律,但不满足交换律。一个四元数可以表示成:\(q=a+bi+cj+dk\),其中\(i^2=j^2=k^2=ijk=-1\)。四元数的加减乘除和复数类似,就是不停应用这些运算规则和分配律、结合律。设向量\(\mathbf{v}=[b,c,d]^T\),用\([a,\mathbf{v}]\)表示四元数\(q=a+bi+cj+dk\)。
有了新的表示方法,对于任意四元数\(q_1=[s,\mathbf{v}]\),\(q_2=[t, \mathbf{u}]\),\(q_1q_2\)的结果是 \[ q_1q_2=[st-\mathbf{v}\cdot\mathbf{u},s\mathbf{u}+t\mathbf{v}+\mathbf{v}\times \mathbf{u}] \] 这个结果也叫做 Graßmann 积。
对于四元数\(q=[s,\mathbf{v}]\),其共轭为\(q^*=[s,-\mathbf{v}]\)。其逆为\(q^{-1}=\frac{q^*}{\parallel q \parallel^2}\)。这样对于单位四元数,其逆就是其共轭四元数。
可以用纯四元数表示一个三维空间的向量\(\mathbf{v}\):\(v=[0, \mathbf{v}]\)。
任意向量\(\mathbf{v}\)绕单位向量定义的旋转轴\(\mathbf{u}\) 旋转\(\theta\)度之后的 \(\mathbf{v}′\) 可以使用四元数乘法来获得。令\(v=[0, \mathbf{v}]\),\(q=[\cos(\frac{1}{2}\theta), \sin(\frac{1}{2}\theta)\mathbf{u}]\),那么: \[ v'=qvq^*=qvq^{-1} \]
可以证明,\(v'\)是一个纯四元数。
根据上面的介绍,你可以从一个单位四元数中提取出旋转角度和旋转轴。
四元数转旋转矩阵
单位四元数对应一种旋转,可以转为旋转矩阵,任意向量 \(\mathbf{v}\)沿着以单位向量定义的旋转轴\(\mathbf{u}\)旋转\(θ\)角度之后的\(\mathbf{v}′\) 可以使用矩阵乘法来获得。令\(a=\cos(\frac{1}{2}\theta)\),\(b=\sin(\frac{1}{2}\theta)u_x\),\(c=\sin(\frac{1}{2}\theta)u_y\),\(d=\sin(\frac{1}{2}\theta)u_z\),那么 \[ \mathbf{v}'=\left[ \begin{matrix} 1-2c^2-2d^2 & 2bc-2ad & 2ac+2bd \\ 2bc+2ad & 1-2b^2-2d^2 & 2cd-2ab \\ 2bd-2ac & 2ab+2cd & 1-2b^2-2c^2 \end{matrix} \right]\mathbf{v} \]
注意旋转和单位四元数不是一一对应的。单位四元数与 3D 旋转之间是2对1满射同态的。关键词:双层覆盖。
四元数插值
对四元数的插值就是对旋转的插值。
Nlerp
线性插值: \[ q_t=\text{Nlerp}(q_0, q_1,t)=\frac{(1-t)q_0+tq_1}{\parallel (1-t)q_0+tq_1 \parallel} \] 缺点是在插值弧度比较大时,角速度变换不均匀效果比较明显。
Slerp
为了解决角速度变换不均匀,可以对角度插值。假设四元数之间的夹角是\(\theta\),有 \[ q_t=\text{Slerp}(q_0,q_1,t)=\frac{\sin(1-t)\theta}{\sin(\theta)}q_0+\frac{\sin(t\theta)}{\sin(\theta)}q_1 \\ \] 四元数之间的夹角可以用点乘法求出: \[ \theta=\cos^{-1}(q_0\cdot q_1) \] 四元数的点乘就是各分量相乘相加。
在\(\theta\)非常小时\(\sin(\theta)\)会非常小,此时应该用Nlerp替代。在\(\theta\)非常小的情况下Nlerp误差非常小。
除此之外,为了确保插值是最短路径,要检查\(\theta\)是否是钝角。如果\(q_0\cdot q_1<0\),那就反转一个四元数,如\(-q_0\),再对\(-q_0\)和\(q_1\)插值。
更多插值见Rerefence。