光栅化
一、三角形光栅化
三角形光栅化就是将三角面片覆盖的像素绘制出来,从而在屏幕上可见。有几个目标需要实现:
不重复的:不重复绘制像素,例如相邻的三角形之间公共边覆盖到的像素应当只被绘制一次。
无缝的:例如相邻的三角形之间光栅化出来应当是没有缝隙的,连续的。
遍历三角形
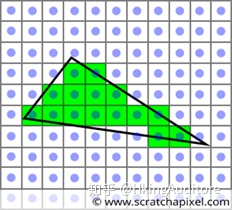
这一步用来确定哪些范围内含有被三角形覆盖的像素。
有几种方法:
- 遍历三角形包围盒范围内像素,逐像素判断是否被三角形覆盖。判断使用的是边界函数算法,也称为半空间法。
- 扫描线法。
最简单就是半空间法,虽然暴力,但是容易并行执行。
边界函数算法
判断点三角形内部
以半空间法为例,最重要的就是判断一个像素点是否在三角形的内部了。如果在内部,我们就插值并着色,否则就丢弃。
三角形每条边所在的直线分别将空间分成了两个部分。通过直线的边界函数的符号,可以判断一个点在直线的左侧还是右侧。如果一个点均在三边的同侧(即符号相同),说明点在三角形内侧;如果规定了三角形的顺序对应的正反,也可以通过符号确定当前三角形是正面还是反面(常用的是三角形逆时针方向为正面)。
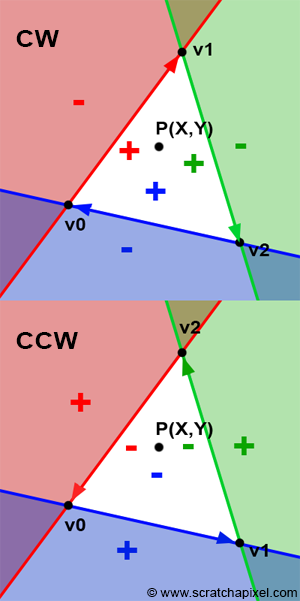
对于边\(AB\),其边界函数为: \[ E_{AB}(P)=(x_B-x_A)(y_P-y_A)-(x_P-x_A)(y_B-y_A) \] 其实本质就是一个叉乘,反映了向量\(AB\)和\(AP\)构成的平行四边形的有向面积。
由此可得: \[ \begin{aligned} E_{AB}(P)>0 \\ E_{BC}(P)>0 \\ E_{CA}(P)>0 \end{aligned} \]
满足上式,说明点在三角形内部。
当点在三角形边上
当边界函数值为0时,说明点可能在三角形的边界上(如图中红色点)。最简单的方法是直接将在三角形边界上的点视作在三角形内部,直接绘制。但是这样做会重复绘制共边上的像素。在不透明渲染中这样没问题,但是在半透明渲染时,多余的绘制会导致颜色不正确。因此需要一些方法来避免重复绘制。
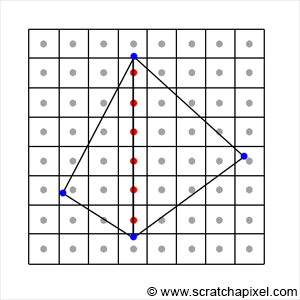
常用top-left规则来渲染在三角形边上的像素,根据所在边的类型不同,选择是否渲染。这个方法对于水密(watertight)的模型是没问题的,但是对于面片(例如一面仅由两个三角面片构成的墙),可能出现边渲染缺失的情况。
边的类型如下图所示(注意三角形顶点顺序!图中将顺时针作为三角形正面,如果你用的是逆时针顺序为正面,就要反过来):
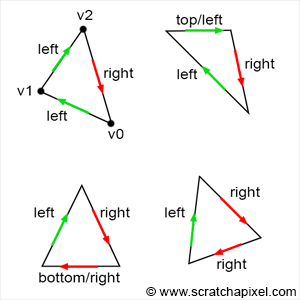
- top边就是完全水平的边,并且其两端点在第三个点的上面。具体来说(以上图顺时针为例),就是边的y坐标差值为0,x坐标差值为正。
- left边就是往上走的边(如果是逆时针,那就往下走,就是反过来嘛)。具体来说(以上图顺时针为例),就是y坐标差值为正。
综上,我们就达成了光栅化第一目标。下面给出伪代码,注意下面的伪代码顶点是定义在逆时针顺序上的,请自行转换:
1 | vec2 edge0 = v[2] - v[1]; |
如何无缝
光栅化第二个目标是无缝。缝隙往往出现在模型的接缝处,并且出现缝的原因往往是精度误差带来的。
如果使用浮点数参与边界函数的计算,误差是无可避免的。对于接缝处的计算,需要判0,这是浮点数不擅长的。而且涉及很多乘法,这会放大误差。有一些方法可以改善,例如先做差再相乘比先相乘再做差更好;双精度浮点数。但这都是治标不治本的。
可以发现,整个光栅化整个过程中(不包括插值和着色),只涉及到乘法和加法(比如边界函数)。因此如果能转换为整数,虽然整体上可能会丢失一些精度,但是这样边界函数结果将不会有误差,接缝处的计算将永远是准确的。
因此对可以预先对三角形三个顶点四舍无入为整数,再进行后续判断。改进后的伪代码如下:
1 | // vec2i是vec2的整数版本,vec2到vec2i转换过程中各分量会四舍五入 |
仅仅一个像素的精度丢失,无伤大雅。
二、直线光栅化
1. 数值微分DDA
根据斜截:\(y=kx+b\)。假设\(k<1\),这样\(y\)增长比\(x\)慢,所以就可以每次向右前进一个像素,判断这个\(x\)坐标下的\(y\)是多少。
对于\(k\)的其它情况,做相应的交换即可。例如\(k>1\),就交换\(x\)和\(y\),就变回\(k<1\)的情况了。
由\(y_{i+1}=k(x+1)+b=(kx+b)+k=y_{i}+k\),可以发现\(x\)每加1,\(y\)加\(k\)即可。代码如下:
1 | void drawlineDDA(int x0,int y0,int x1,int y1, Framebuffer &fb) { |
涉及浮点数的计算,效率较慢。
2. 中点画线算法
将直线写成\(Ax+By+C=0\)。整个方程将平面划分成三部分:\(Ax+By+C\)分别大于等于小于0三部分。当\(B\)为正数时,\(Ax+By+C\)大于0代表点\((x,y)\)在直线上面;小于0在下面;等于0在直线上。
以\(0<k<1\)为例,\(x\)增加1时,\(y\)要么增加1,要么不变。因此通过判断\(y\)和\(y+1\)中点\(y+0.5\)相对直线位置,就可以知道哪个离直线更近。
1 | // 前面乘B的目的是让B系数为正 |
下面进行一些优化:
如果已知下一点画在\((x_i+1,y_i+1)\),那么接下来要考虑\(M_1(x_i+2,y_i+1.5)\),带入\(M_1\)到直线方程,有 \[ d_1=A(x_i+2)+B(y_i+1.5)+C=(A(x_i+1)+B(y_i+0.5)+C)+A+B=d_0+A+B \]
如果已知下一个点画在\((x_i+1,y_i)\),那么接下来要考虑\(M_1(x_i+2,y_i+0.5)\),带入\(M_1\)到直线方程,有 \[ d_1=A(x_i+2)+B(y_i+0.5)+C=(A(x_i+1)+B(y_i+0.5)+C)+A=d_0+A \]
因此判断中点和直线相对位置这里可以用增量的方式计算,避免了乘法。
1
2
3
4
5
6
7
8
9
10
11
12
13// 初值
double d = A * (x0 + 1) + B * (y0 + 0.5) + C;
// 前面乘B的目的是让B系数为正
if(B * d < 0) {
// 中点在直线下面,说明(x+1,y+1)离直线更近
y = y + 1;
d = d + A + B;
} else {
// 中点在直线上面,说明(x+1,y)离直线更近
y = y;
d = d + A;
}
x = x + 1;
可以发现只有\(0.5\)这个浮点数,可以全部乘以2,避免浮点数的使用,全部用整数代替。
1
2
3
4
5
6
7
8
9
10
11
12
13// 初值
int d = 2 * A * (x0 + 1) + B * (2 * y0 + 1) + 2 * C;
// 前面乘B的目的是让B系数为正
if(B * d < 0) {
// 中点在直线下面,说明(x+1,y+1)离直线更近
y = y + 1;
d = d + 2 * (A + B);
} else {
// 中点在直线上面,说明(x+1,y)离直线更近
y = y;
d = d + 2 * A;
}
x = x + 1;
对于\(k\)的其它情况,做各种转化为\(0<k<1\)即可。注意如果\(k<0\),中点判断规则是反过来的。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32void drawlineMid(int x0,int y0,int x1,int y1, Framebuffer &fb) {
int dx = abs(x0 - x1), dy = abs(y0 - y1);
if(dx < dy) {
swap(x0, y0);
swap(x1, y1);
}
if(x0 > x1) {
swap(x0, x1);
swap(y0, y1);
}
int A = y1 - y0;
int B = x0 - x1;
int C = -(A * x0 + B * y0);
int sgn = y0 < y1 ? 1 : -1;
int d = 2 * A * (x0 + 1) + B * (2 * y0 + sgn) + 2 * C;
int y = y0;
for(auto x = x0 ; x <= x1 ; ++x) {
if(dx < dy) {
fb.set(y, x);
} else {
fb.set(x, y);
}
if(sgn * B * d < 0) {
d += 2 * (A + sgn * B);
y += sgn;
} else d += 2 * A;
}
}
完整代码
1 |
|
参考
fundamentals of computer graphics 4th, 11.2.4: Perspective Correct Interpolation
Rasterization: a Practical Implementation (The Rasterization Stage) (scratchapixel.com)