法线矩阵和TBN矩阵
法线变换矩阵
经过模型变换后,法线也要跟着一起变换。假设物体发生了缩放形变,如果对法线应用相同的变换,可能会得到错误结果:
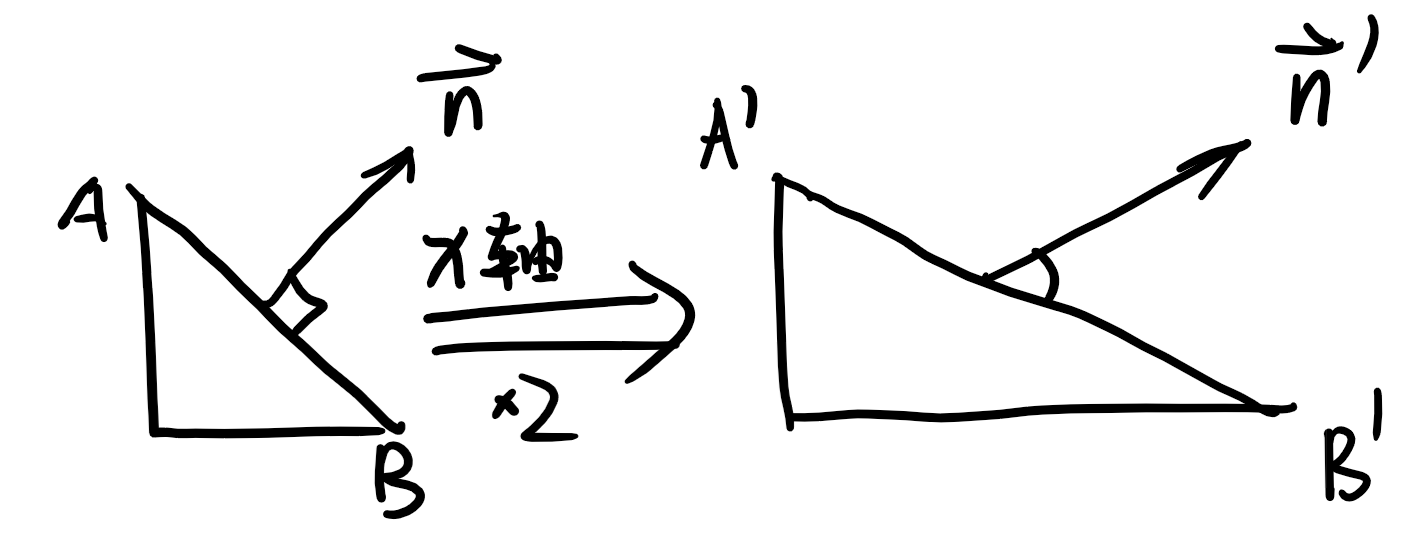
假设平面上一条切线\(\mathbf{t}\)(比如说,向量\(\text{AB}\)),变换矩阵为\(M\)。经过变换后\(\mathbf{t}'=M\mathbf{t}\)(变换后\(\mathbf{t}'=M\text{B}-M\text{A}=M(\text{B}-\text{A})=M\mathbf{t}\))。变换前后,\(\mathbf{n}\)都应该和切线垂直,可得: \[ \text{dot}(\mathbf{t'}, \mathbf{n}')=\text{dot}(M\mathbf{t},N\mathbf{n})=\mathbf{t}^TM^TN\mathbf{n}=0 \] 很显然,当\(M^TN\)为单位矩阵时上式成立。可得\(N=(M^{T})^{-1}\)。因此对法线应该作用变换矩阵转置的逆,可以保持法线垂直于变换后的平面。可以看出,如果只有平移和旋转,那么\(N=M\)(平移对法线没影响,旋转矩阵的转置即为逆),这也说明了法线变换问题是形变带来的。
TBN矩阵
用途
为物体添加细节的方法除了提高模型的精度,可以使用法线贴图。法线贴图利用图片的三通道存储法线的三个分量。法线贴图可以存储模型空间下法线的值,这样出来的法线贴图看起来就五彩缤纷;也可以存储为在切线空间下的值,在这个空间中,平面的法线为N轴,u、v的方向为T、B轴,如下图所示:
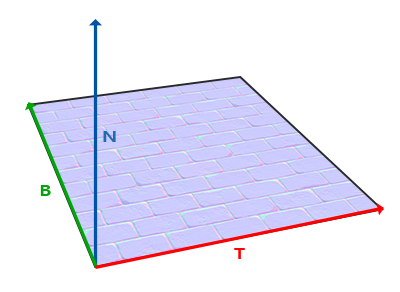
在法线贴图中三个通道RGB分别用于存储T(tangent)、B(bitangent)、N(normal)轴的分量。
模型空间下法线存储贴图是法线变化更加平滑,缺点是一张贴图只能对应一个模型。而切线空间下的法线贴图可以在任何模型之间切换,而且大部分法线都和N靠的比较近(更加靠近\((0,0,1)\),这就是为什么大部分法线贴图都偏蓝),更加便于压缩。
因此,只要能求出在模型空间下T、B、N轴的向量,按照贴图中记录的分量线性组合就可以得到模型空间下的法线。TBN矩阵就是贴图中向量到世界空间的变换矩阵。注意,T、B、N是正交的单位坐标系,因此TBN矩阵也是正交矩阵。
求法
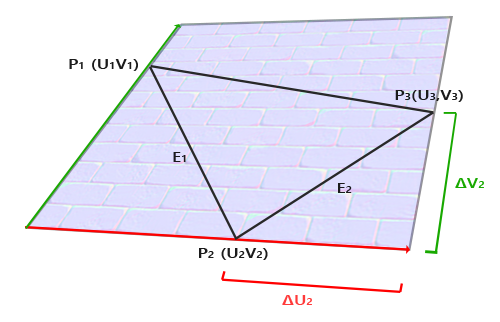
因为U,V方向分别是T,B轴,如上图所示,模型空间下三角面片边\(E_1\)和\(E_2\)可以表示成\(T\)和\(B\)轴的线性组合: \[ \left[ \begin{matrix} E_1\\ E_2 \end{matrix} \right]=\left[ \begin{matrix} \Delta U_1 & \Delta V_1\\ \Delta U_2 & \Delta V_2 \end{matrix} \right] \left[ \begin{matrix} T\\ B \end{matrix} \right] \] 很显然,我们除了\(T\)、\(B\),其它信息都知道,所以可以得到: \[ \left[ \begin{matrix} \Delta U_1 & \Delta V_1\\ \Delta U_2 & \Delta V_2 \end{matrix} \right]^{-1} \left[ \begin{matrix} E_1\\ E_2 \end{matrix} \right]= \frac{1}{\Delta U_1\Delta V_2 - \Delta U_2\Delta V_1} \left[ \begin{matrix} \Delta V_2 & -\Delta V_1\\ -\Delta U_2 & \Delta U_1 \end{matrix} \right] \left[ \begin{matrix} E_1\\ E_2 \end{matrix} \right]= \left[ \begin{matrix} T\\ B \end{matrix} \right] \]
这样就得到T,B轴,加上顶点法线N,就可以构造TBN矩阵了。等等!其实还没完。有以下几点需要注意:
- 顶点法线\(\neq\)平面法线:平面法线是垂直于面片的向量;顶点法线可以是任意的,比如艺术家的调整、相邻平面法线的平均(平滑)...
- 这样求出的T、B、N不一定正交。这是很正常的,可能物体被拉伸,可能uv映射不是完美对应的,加上N不是平面法线而是顶点法线,大部分情况下这样算出来的T、B、N都不正交。
TBN正交是很重要的,如果不正交,变换后的法线可能被拉伸。而理想情况下(TBN为正交矩阵)应该只是对法线进行旋转而已。
因此还应当进行格拉姆-施密特正交化(\(T'\)代表上面求出的,\(T\)和\(B\)是真正的切线和副切线): \[ \begin{aligned} T &= \text{normalize}(T-(N\cdot T')N) \\ B &= N \times T \end{aligned} \] 上式其实就是正交分解的逆过程。
最后,假设从法线贴图中得到的法线是\(n\)(注意贴图中的法线非负做了偏移,真正的法线为\(2n-1\)),那么真正模型空间的法线为: \[ n_xT+n_yB+n_zN=[T,B,N]n \] 这个\([T,B,N]\)就是TBN矩阵。
在加载模型时,就可以对每个面片计算出T和B。因此T,B和N都是作为顶点属性传入着色器。为了保证TBN正交,可以在片元着色器中正交化后构造为TBN矩阵后使用。